|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Grete Hermann John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington James D. Watson John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
The Two-Slit Experiment and "One Mystery" of Quantum Mechanics
Richard Feynman said that the two-slit experiment contains the "one mystery" of quantum mechanics.
I will take just this one experiment, which has been designed to contain all of the mystery of quantum mechanics, to put you up against the paradoxes and mysteries and peculiarities of nature one hundred per cent. Any other situation in quantum mechanics, it turns out, can always be explained by saying, 'You remember the case of the experiment with the two holes? It's the same thing'.We will show that the (one) mystery of quantum mechanics is how mere "probabilities" can causally control (statistically) the positions of material particles - how immaterial information can affect the material world. This remains a deep metaphysical mystery. The two-slit experiment was until recent years for the most part a thought experiment, since it is difficult to build an inexpensive demonstration, but its predictions have been verified in many ways since the 1960's, primarily with electrons. Recently, extremely sensitive CCDs used in photography have been used to collect single-photon events, establishing experimentally everything that Albert Einstein imagined, merely by thinking about it, as early as 1905. 
Light at the yellow dot slowly disappears as the second slit opens! Adding light causes some light to disappear! 
Young's 1802 drawing of wave interference
Water waves in a pond Dr. Quantum and the two-slit experiment 




Why interference patterns show up when both slits are open, even when particles go through just one slit, though we cannot know which slit or we lose the interference

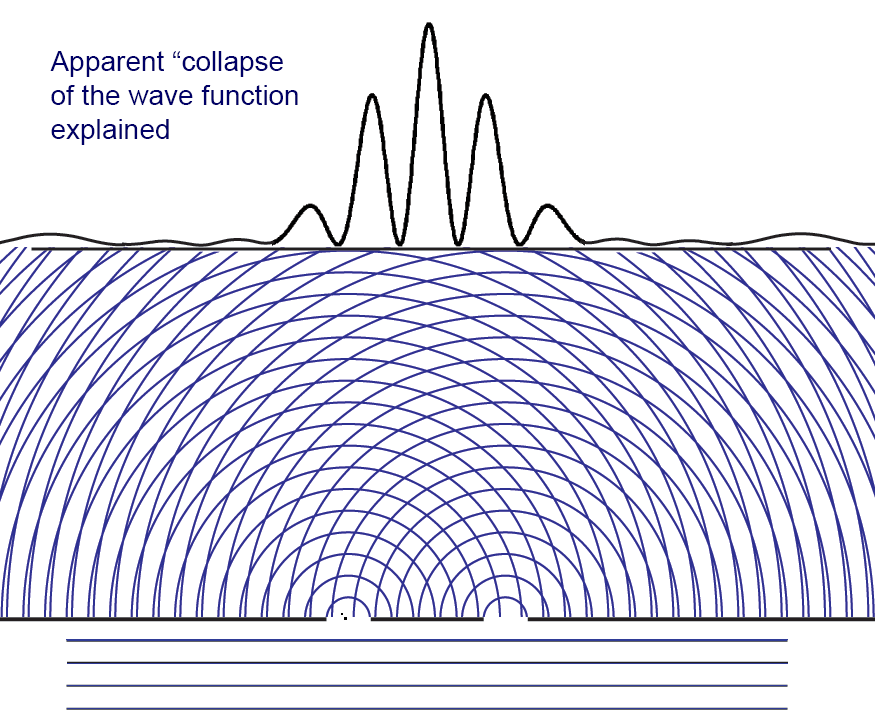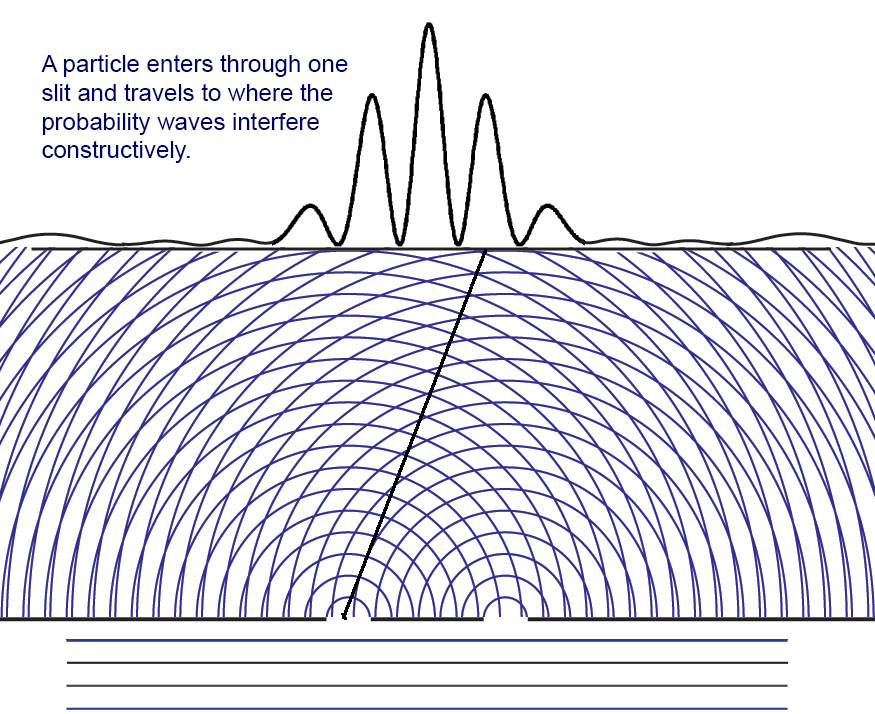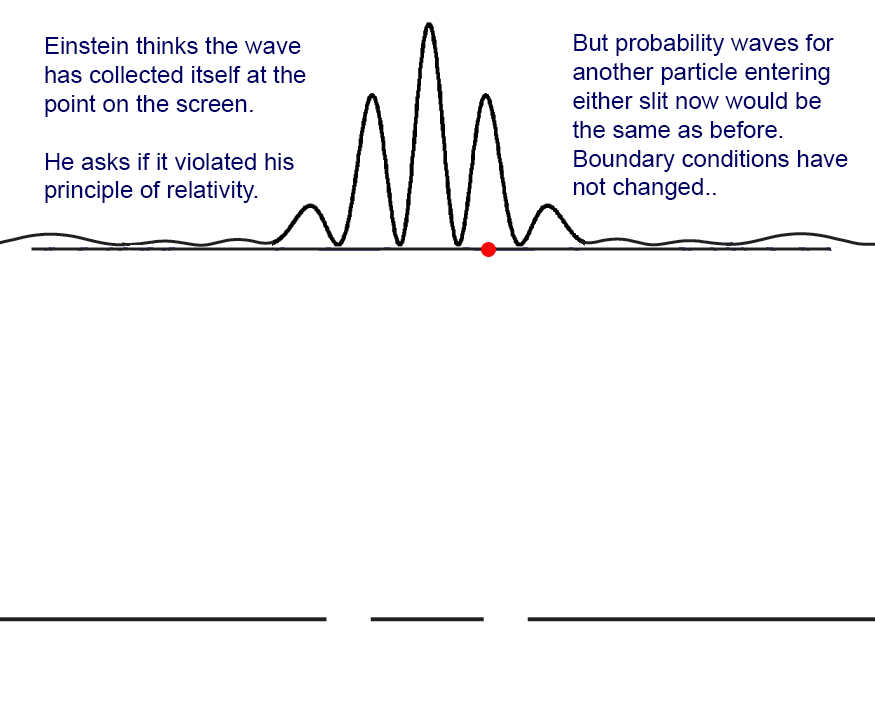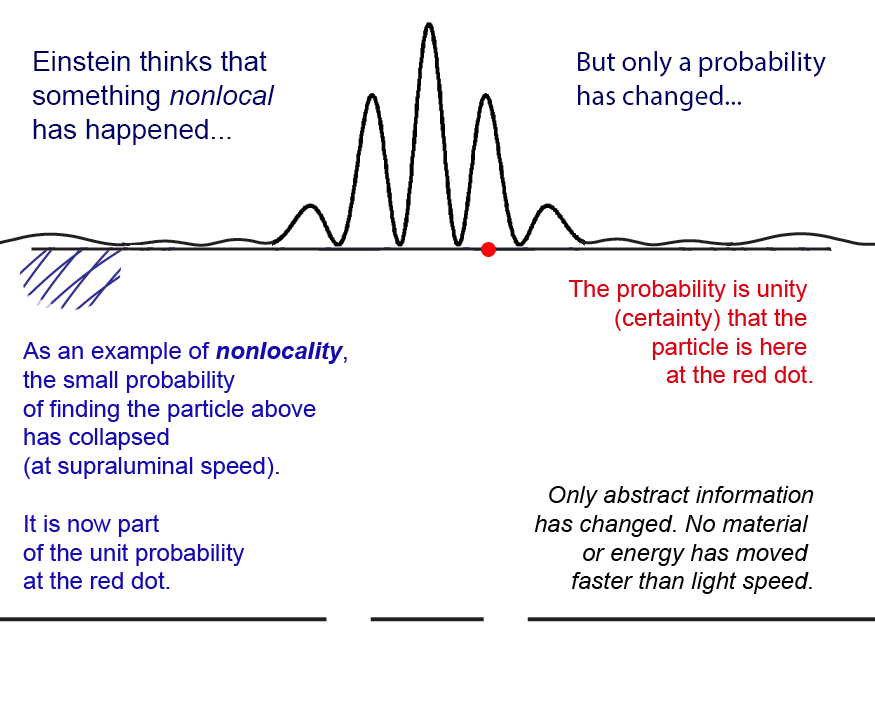
Collapse of the Wave Function
But how do we interpret the notion of the "collapse" of the wave function? At the moments just before a particle is detected at the CCD or photographic plate, there is a finite non-zero probability that the photon could be detected anywhere that the modulus (complex conjugate squared) of the probability amplitude wave function has a non-zero value.
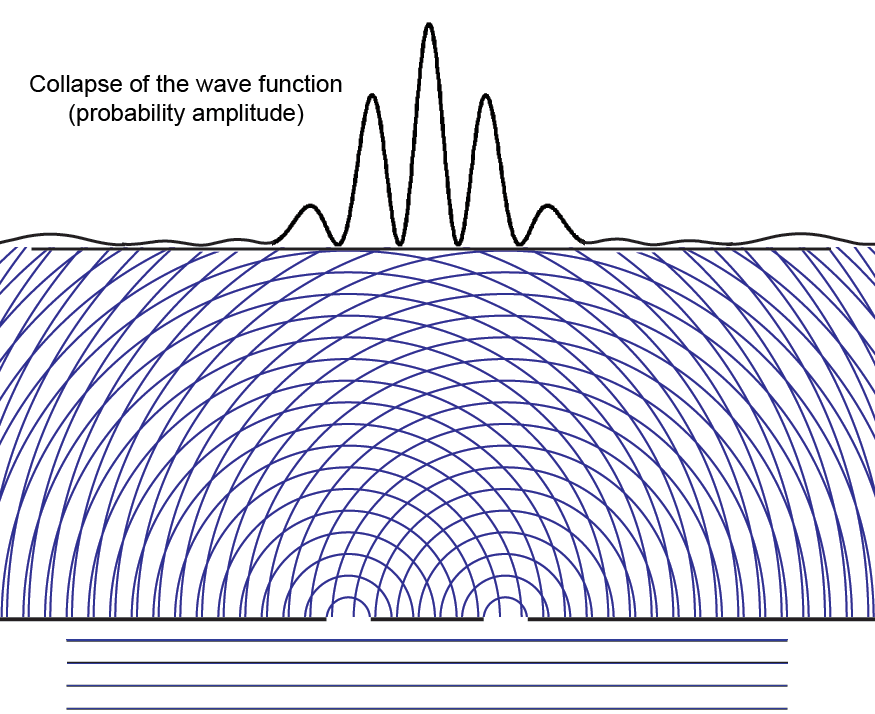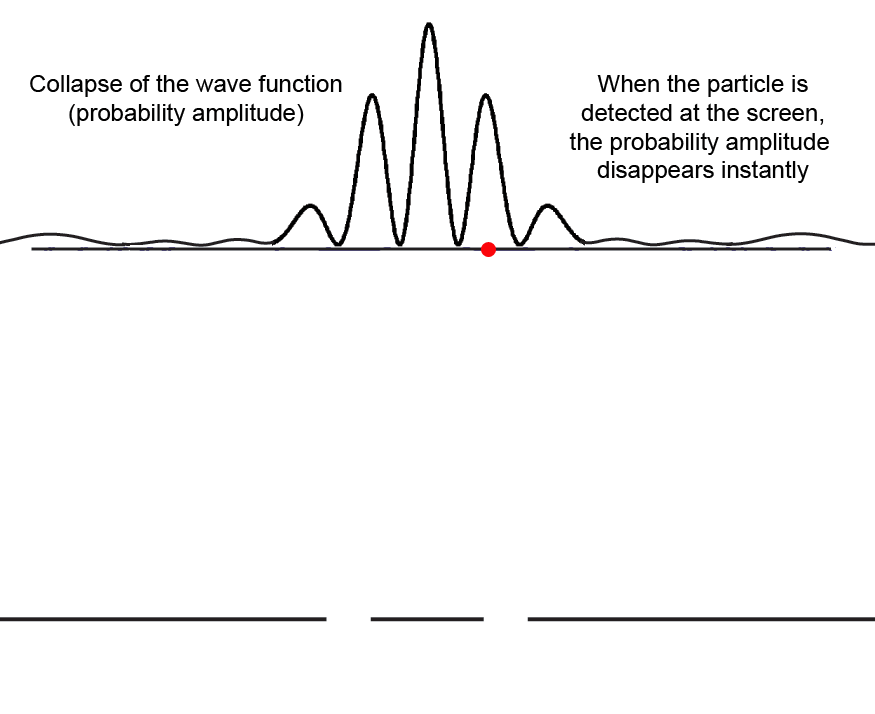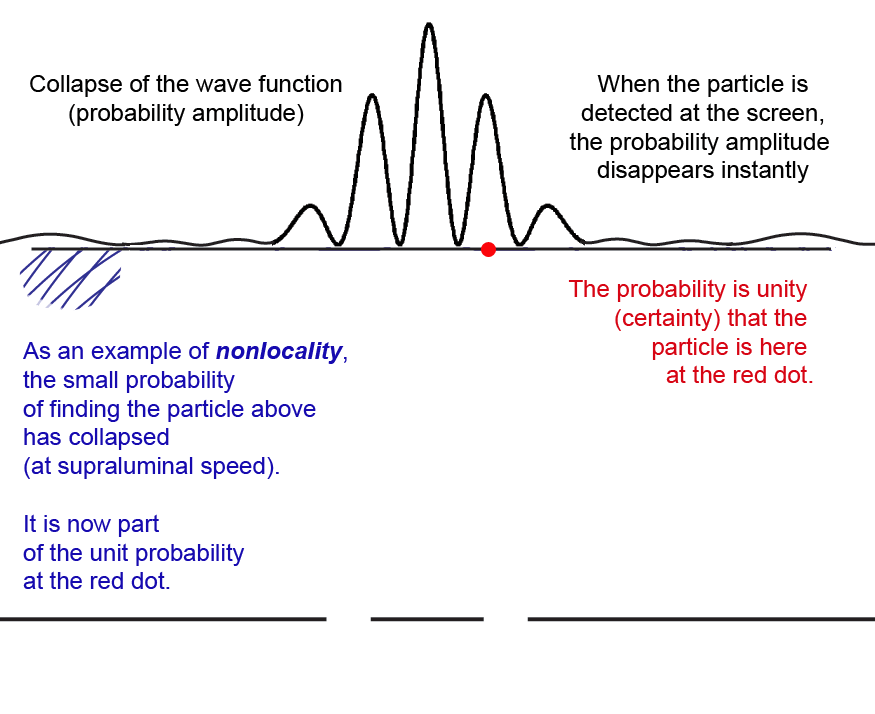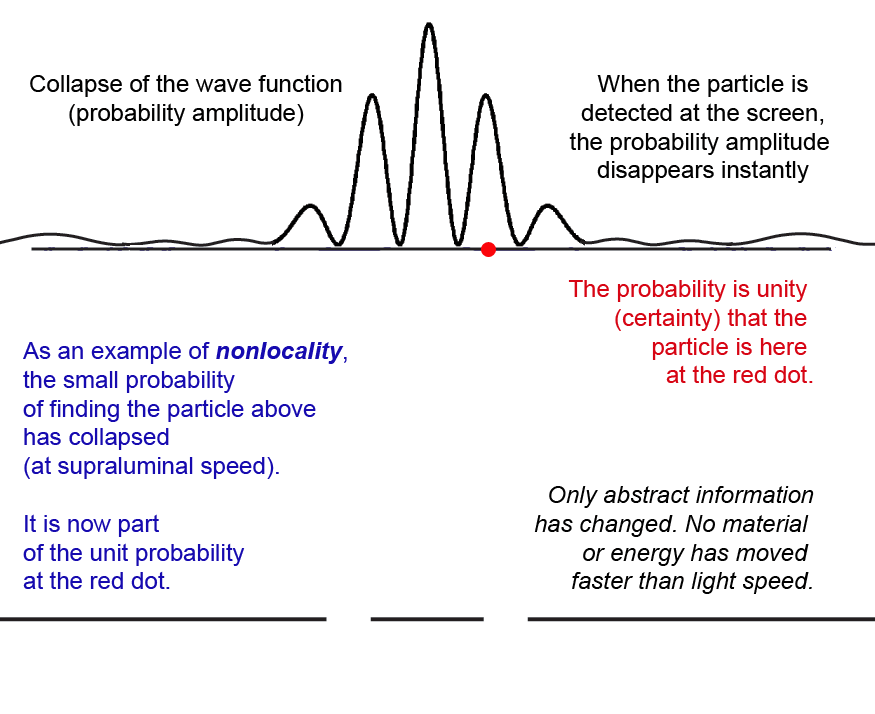
If our experiment were physically very large (and it is indeed large compared to the atomic scale), we can say that the finite probability of detecting (potentially measuring) the particle at position x1 on the screen "collapses" (goes to zero) and reappears as part of the unit probability (certainty) that the particle is at x2, where it is actually measured.
Since the collapse to zero of the probability at x1 is instantaneous with the measurement at x2, critics of quantum theory like to say that something traveled faster than the speed of light. This is most clear in the nonlocality and entanglement aspects of the Einstein-Podolsky-Rosen experiment. But the sum of all the probabilities of measuring anywhere on the screen is not a physical quantity, it is only immaterial information that "collapses" to a point.
Here is what happens to the probability amplitude wave function (the blue waves) when the particle is detected at the screen (either a photographic plate or CCD) in the second interference fringe to the right (red spot). The probability simply disappears instantly.
Animation of a wave function collapsing - click to restart
History
The first suggestion of two possible directions through a slit, one of which disappears ("collapses?") when the other is realized (implying a mysterious "nonlocal" correlation between the directions), was made by Albert Einstein at the 1927 Solvay conference on "Electrons and Photons." Niels Bohr remembered the occasion with a somewhat confusing description.
Here is his 1949 recollection:
At the general discussion in Como, we all missed the presence of Einstein, but soon after, in October 1927, I had the opportunity to meet him in Brussels at the Fifth Physical Conference of the Solvay Institute, which was devoted to the theme "Electrons and Photons."Although Bohr seems to have missed Einstein's point completely, Werner Heisenberg at least came to explain it well. In his 1930 lectures at the University of Chicago, Heisenberg presented a critique of both particle and wave pictures, including a new example of nonlocality that Einstein had apparently developed since 1927. It includes Einstein's concern about "action-at-a-distance" that might violate his principle of relativity, and anticipates the Einstein-Podolsky-Rosen paradox. Heisenberg wrote: In relation to these considerations, one other idealized experiment (due to Einstein) may be considered. We imagine a photon which is represented by a wave packet built up out of Maxwell waves. It will thus have a certain spatial extension and also a certain range of frequency. By reflection at a semi-transparent mirror, it is possible to decompose it into two parts, a reflected and a transmitted packet. There is then a definite probability for finding the photon either in one part or in the other part of the divided wave packet. After a sufficient time the two parts will be separated by any distance desired; now if an experiment yields the result that the photon is, say, in the reflected part of the packet, then the probability of finding the photon in the other part of the packet immediately becomes zero. The experiment at the position of the reflected packet thus exerts a kind of action (reduction of the wave packet) at the distant point occupied by the transmitted packet, and one sees that this action is propagated with a velocity greater than that of light. However, it is also obvious that this kind of action can never be utilized for the transmission of signals so that it is not in conflict with the postulates of the theory of relativity.Clearly the "kind of action (reduction of the wave packet)" described by Heisenberg is the same "mysterious" influence that the wave function has over the places that the particle will be found statistically in a large number of experiments, including our canonical "mystery," the two-slit experiment. Apart from the statistical information in the wave function, quantum mechanics gives us only vague and uncertain information about any individual particle. This is the true source of Heisenberg's uncertainty principle. It is the reason that Einstein correctly describes quantum mechanics as "incomplete." Quantum mechanics does not prove that the particle actually has no position at each instant and a path that conserves its momentum, spin, and other conserved properties. In Einstein's view of "objective reality," the particle has those properties, even if quantum mechanics prevents us from knowing them - without a measurement that destroys their interference capabilities or "decoheres" them.
Some Other Animations of the Two-Slit Experiment
None of these animations, viewed many millions of times, can explain why a particle entering one slit when both are open exhibits the properties of waves characteristic of two open slits. It remains Feynman's "one mystery" of quantum mechanics.
PBS Digital Studios
Veritasium Veritasium Wave-Particle Duality Animation One good thing in this animation is that it initially shows only particles firing at the slits. This is important historically because Isaac Newton thought that light was a stream of particles traveling along a light ray. He solved many problems in optics by tracing light rays through lenses. But without a clear verbal explanation it is hard to follow.
The Fresnel-Arago Version of the Two-slit Experiment
We look at the Hamamatsu Photonics version of the Fresnel-Arago two-slit experiment.
This experiment puts polarizers at +45 and -45 degrees over the left and right slits.
Let's see how the wave function explains the different results with a third polarizer (analyzer) intermediate between the slits and the screen in vertical or horizontal orientation.
As Paul Dirac explains, a 45 degree polarizer produces photons in a linear combination (or superposition) of vertical |v> and horizontal [h> states.

| d > = ( 1/√2) | v > + ( 1/√2) | h >
So the photons passing through either the left or right slit are 50% vertical and 50% horizontal.
But note that the vertical photons going through both slits are in phase (pointing up), while the horizontal photons going through the right slit (+45 pointing right |→>) are out of phase with those going through the left slit (-45 pointing left |←>).
So when the intermediate polarizer (analyzer) is vertical, it passes photons that are in phase | ↑> |↑> and they constructively interfere, as the Hamamatsu diagrams explain. Horizontally polarized photons are absorbed. The central fringe is bright.
 When the intermediate polarizer is horizontal, vertically polarized photons are absorbed, left and right photons passing straight through the slits are out of phase, |←> and |→>, and so destructively interfere, |←> |→>. The central fringe is now dark. When the angle of photons going through the slits is to the left or right, the path of light for one slit is longer, and the phase difference goes to zero at the bright fringes on either side of the dark center.
When the intermediate polarizer is horizontal, vertically polarized photons are absorbed, left and right photons passing straight through the slits are out of phase, |←> and |→>, and so destructively interfere, |←> |→>. The central fringe is now dark. When the angle of photons going through the slits is to the left or right, the path of light for one slit is longer, and the phase difference goes to zero at the bright fringes on either side of the dark center.
 The waves (or wave functions) tell us about the probabilities of finding photons, and the angles at which they leave the slits determine their relative phases.
The waves (or wave functions) tell us about the probabilities of finding photons, and the angles at which they leave the slits determine their relative phases.
For Teachers
For Scholars
|
||||||