Biologist Charles Sherrington had speculated in the 1950's that information might be stored in the brain in microtubules, lattices of tubulin dimers. Hameroff decided that the bits of information might be stored in discrete states of tubulin, interacting by dipole-dipole interactions with neighboring tubulin states. These structures are orders of magnitude smaller than the biological cells, providing vast amounts of potential information storage.

A hydrophobic pocket in tubulin develops electron resonance rings in the pocket. Single electrons in each ring repel each other, as the net dipole moment of their electron cloud flips under external London force oscillations.

Although Hameroff did not provide a specific read-write mechanism, he modeled the tubulin states as cellular automata (these "cells" are the fundamental units of John Conway's "Game of Life") that would need to change states at synchronized time steps, governed by the coherent voltage oscillations. (Although brain wave oscillations are well-known, those observed are at very low frequencies compared to the proposed oscillation in the microtubules - 10⁹/sec.) Each automaton cell interacts with its neighbor cells at discrete, synchronized time steps, the state of each cell at any particular time step determined by its state and its neighbor cell states at the previous time step, and rules governing the interactions. In such ways, using simple neighbor interactions in simple lattice grids, cellular automata might perform complex computations and generate complex patterns.

The estimated total information processing in the tubulin of a single neuron is of the same order of magnitude as that for the entire brain, if storage is at the synapses of the neural networks. This surprised (and annoyed) some cognitive scientists, but again, no plausible read/write mechanism was proposed for either computational model.

In 1989, Roger Penrose published The Emperor's New Mind, which was followed in 1994 by Shadows of the Mind. There he proposed a solution to the measurement problem in quantum mechanics by extending the standard framework's idea of a random collapse (or reduction) of the wave function with a more "objective" collapse he called "objective reduction" (OR).

Objective reduction would terminate the deterministic evolution of the wave function predicted by the Schrödinger equation. (Another scheme to force the collapse was proposed by Ghirardi, Rimini, and Weber.) Penrose initially looked to quantum gravity as the driving force behind OR.

Note that the traditional connection between consciousness and the collapse of the wave-function was the result of early work by John von Neumann and Eugene Wigner. They assumed that a conscious observer was needed to make a measurement (producing at least one bit of information). Without an observer, goes their argument, the wave-function would not collapse, leading to paradoxes like Schrödinger's Cat. Many other physicists deny that a conscious observer is necessary for a physical measurement. [See our solution to the measurement problem.]

Hameroff and Penrose began working together in the 1990's to develop an "orchestrated" version of objective reduction.

According to Orch OR, the (objective) reduction is not the entirely random process of standard theory, but acts according to some non-computational new physics (see Penrose 1989, 1994). The idea is that consciousness is associated with this (gravitational) OR process, but occurs significantly only when the alternatives are part of some highly organized structure, so that such occurrences of OR occur in an extremely orchestrated form. Only then does a recognizably conscious event take place. On the other hand, we may consider that any individual occurrence of OR would be an element of proto-consciousness.

The OR process is considered to occur when quantum superpositions between slightly differing space-times take place, differing from one another by an integrated space-time measure which compares with the fundamental and extremely tiny Planck (4-volume) scale of space-time geometry. Since this is a 4-volume Planck measure, involving both time and space, we find that the time measure would be particularly tiny when the space-difference measure is relatively large (as with Schrödinger's cat), but for extremely tiny space-difference measures, the time measure might be fairly long, such as some significant fraction of a second. We shall be seeing this in more detail shortly, together with its particular relevance to microtubules. In any case, we recognize that the elements of proto-consciousness would be intimately tied in with the most primitive Planck-level ingredients of space-time geometry, these presumed 'ingredients' being taken to be at the absurdly tiny level of 10⁻³⁵m and 10⁻⁴³s, a distance and a time some 20 orders of magnitude smaller than those of normal particle-physics scales and their most rapid processes. These scales refer only to the normally extremely tiny differences in space-time geometry between different states in superposition, and OR is deemed to take place when such space-time differences reach the Planck level. Owing to the extreme weakness of gravitational forces as compared with those of the chemical and electric forces of biology, the energy E_G is liable to be far smaller than any energy that arises directly from biological processes. However, E_G is not to be thought of as being in direct competition with any of the usual biological energies, as it plays a completely different role, supplying a needed energy uncertainty that then allows a choice to be made between the separated space-time geometries. It is the key ingredient of the computation of the reduction time τ. Nevertheless, the extreme weakness of gravity tells us there must be a considerable amount of material involved in the coherent mass displacement between superposed structures in order that τ can be small enough to be playing its necessary role in the relevant OR processes in the brain. These superposed structures should also process information and regulate neuronal physiology. According to Orch OR, microtubules are central to these structures, and some form of biological quantum computation in microtubules (most probably primarily in the more symmetrical A-lattice microtubules) would have to have evolved to provide a subtle yet direct connection to Planck-scale geometry, leading eventually to discrete moments of actual conscious experience.

("Consciousness in the Universe: Neuroscience, Quantum Space-Time Geometry and Orch OR," Journal of Cosmology, 2011, Vol. 14)

Hameroff notes that the geometry of CaMKII - a snow-flake shaped double hexagon of twin hexameric rings - and the diameter - 20nm - make the CaMKII a nice fit with microtubules - 15nm internal diameter and 25nm external (and up to 25 microns in length!).

Each monomer is an EF hand motif consisting of two alpha-helices linked by a short "loop region." The helices can each bind two Ca²⁺ ions, and change their configuration like an index finger and thumb to become an active Ca²⁺ - Calmodulin complex. Each of the kinase monomers can activate separately, phosphorylating (or not) a substrate protein. So Hameroff points out that the twelve units in the holoenzyme can encode 12 bits of digital information.

He says:

In this paper we evaluated possible information inputs to microtubules in the context of brain neuronal memory encoding and long-term potentiation (LTP). A key intermediary in LTP involves the hexagonal holoenzyme calcium-calmodulin kinase II. When activated by synaptic calcium influx, the snowflake-shaped CaMKII extends sets of 6 foot-like kinase domains outward, each domain able to phosphorylate a substrate or not (thus convey 1 bit of information). As CaMKII activation represents synaptic information, subsequent phosphorylation by CaMKII of a particular substrate may encode memory, e.g. as ordered arrays of 6 bits (one ‘byte’). We used molecular modeling to examine feasibility of collective phosphorylation (and thus memory encoding) by CaMKII kinase domains of tubulins in a microtubule lattice.

We show, first, complementary electrostatics and mutual attraction between individual CaMKII kinase domains and tubulin surfaces. We also demonstrate two plausible sites for direct phosphorylation of tubulin by a CaMKII kinase domain, and calculate binding energies in the range of 6 to 36 kcal/mol per CaMKII-tubulin phosphorylation event. This indicates encoding which is robust against degradation, yet inexpensive, requiring on the order of 2% of overall brain metabolism for maximal encoding in all 10¹¹ neurons.

We then compare size and hexagonal configuration of the six extended foot-like kinase domains of activated CaMKII with hexagonal lattices of tubulin proteins in MTs. We find that CaMKII size and geometry of 6 extended kinase domains precisely match hexagonal arrays of tubulin in both A-lattice and B-lattices.

Conclusion. We demonstrate a feasible and robust mechanism for encoding synaptic information into structural and energetic changes of microtubule (MT) lattices by calcium-activated CaMKII phosphorylation. We suggest such encoded information engages in ongoing MT information processes supporting cognition and behavior, possibly by generating scale-free interference patterns via reaction-diffusion or other mechanisms. As MTs and CaMKII are widely distributed in eukaryotic cells, the hexagonal bytes and trytes suggested here may reflect a real-time biomolecular information code akin to the genetic code.

("Cytoskeletal Signaling: Is Memory Encoded in Microtubule Lattices by CaMKII Phosphorylation?," PLoS Comput Biol., 2012 March; 8(3): e1002421.)

Conscious “free will” is problematic because (1) brain mechanisms causing consciousness are unknown, (2) measurable brain activity correlating with conscious perception apparently occurs too late for real-time conscious response, consciousness thus being considered “epiphenomenal illusion,” and (3) determinism, i.e., our actions and the world around us seem algorithmic and inevitable.

The Penrose–Hameroff theory of “orchestrated objective reduction (Orch OR)” identifies discrete conscious moments with quantum computations in microtubules inside brain neurons, e.g., 40/s in concert with gamma synchrony EEG. Microtubules organize neuronal interiors and regulate synapses. In Orch OR, microtubule quantum computations occur in integration phases in dendrites and cell bodies of integrate-and-fire brain neurons connected and synchronized by gap junctions, allowing entanglement of microtubules among many neurons. Quantum computations in entangled microtubules terminate by Penrose “objective reduction (OR),” a proposal for quantum state reduction and conscious moments linked to fundamental spacetime geometry. Each OR reduction selects microtubule states which can trigger axonal firings, and control behavior. The quantum computations are “orchestrated” by synaptic inputs and memory (thus “Orch OR”).

If correct, Orch OR can account for conscious causal agency, resolving problem 1. Regarding problem 2, Orch OR can cause temporal non-locality, sending quantum information backward in classical time, enabling conscious control of behavior. Three lines of evidence for brain backward time effects are presented. Regarding problem 3, Penrose OR (and Orch OR) invokes non-computable influences from information embedded in spacetime geometry, potentially avoiding algorithmic determinism. In summary, Orch OR can account for real-time conscious causal agency, avoiding the need for consciousness to be seen as epiphenomenal illusion. Orch OR can rescue conscious free will.

("How quantum brain biology can rescue conscious free will," Frontiers in Integrative Neuroscience, 2012, October 12.)

Hameroff argues that his Orch-OR theory provides the model for consciousness and causal agency needed for "conscious free will."

Orch-OR also addresses the problem of classical determinism (the major impediment to belief in free will is that every action is pre-determined). Hameroff says:

Is the universe unfolding (in which case free will is possible), or does it exist as a “block universe” with pre-determined world-lines, our actions pre-determined by algorithmic processes? In Orch OR, consciousness unfolds the universe. The selection of states, according to Penrose, is influenced by a non-computable factor, a bias due to fine scale structure of spacetime geometry. According to Orch OR, conscious choices are not entirely algorithmic.

("How quantum brain biology can rescue conscious free will," Frontiers in Integrative Neuroscienc, 2012, October 12.)

But the major problem with free will that Hameroff hopes to solve is the objection raised by the Libet experiments that consciousness comes "too late". He says that Orch-OR can send quantum information backward in time to resolve this problem:

Does consciousness come too late?

Brain electrical activity appearing to correlate with conscious perception of a stimulus can occur after we respond to that stimulus, seemingly consciously. Accordingly, consciousness is deemed epiphenomenal and illusory (Dennett, Wegner,). However evidence for backward time effects in the brain (Libet et al., Bem, Ma et al.), and in quantum physics (e.g., to explain entanglement, Penrose, Aharonov and Vaidman, Bennett and Wiesner) suggest that quantum state reductions in Orch-OR can send quantum information backward in (what we perceive as) time, on the order of hundreds of milliseconds. This enables consciousness to regulate axonal firings and behavioral actions in real-time, when conscious choice is felt to occur (and actually does occur), thus rescuing consciousness from necessarily being an epiphenomenal illusion.

("How quantum brain biology can rescue conscious free will.")

Exactly how the science-fiction-like idea of sending information back in time works, that something comes back from the future without creating infinitely recursive time loops, is not made clear. Hameroff discusses three cases, of which two at least are unlikely to involve information going backward in time, the Einstein-Podolsky-Rosen experiment and the Libet experiments.

In the time evolution of an entangled two-particle state according to the Schrödinger equation, we can visualize it - as we visualize the single-particle wave function - as collapsing when a measurement is made. The discontinuous "jump" is also described as the "reduction of the wave packet." This is apt in the two-particle case, where the superposition of | + - > and | - + > states is "projected" or "reduced: to one of these two-particle states, and then further reduced to the product of independent one-particle states.

In the two-particle case (instead of just one particle making an appearance), when either particle is measured we know instantly those properties of the other particle that satisfy the conservation laws, including its location equidistant from, but on the opposite side of, the source, and its other conserved properties such as spin. No information need be "transmitted" for the experimenter to know this information.

And it is incorrect to say that one particle - A - is sent one way and another particle - B - is sent the other way, so that when A is measured, information must be sent to B. Nothing is known until one is measured - and that either one - since they are indistinguishable particles.

Compare the collapse of the two-particle probability amplitude above to the single-particle collapse here.

Finally, since the two particles, once measured, are in a spacelike separation,there is no clear "backward-in-time" or "forward-in-time" relation between them. As first pointed out by C.W.Rietdijk in 1966, then by Hilary Putnam a year later, and Roger Penrose in his 1989 The Emperor's New Mind, in different reference frames A can occur before B or vice versa.

John Bell suggested there might be a preferred frame to analyze the problem of entanglement and nonlocality. The preferred frame is the one in which particles A and B are measured simultaneously, which is what happens from the particles' viewpoint.

To account for his results, [Libet] further concluded that subjective information is referred backwards in time from the time of neuronal adequacy to the time of the EP (Figure ​(Figure9B).9B). Libet's backward time assertion was disbelieved and ridiculed (e.g., Churchland (1981), Pockett (2002), but never refuted (Libet, 2002, 2003).

("How quantum brain biology can rescue conscious free will.")

Moreover, the more familiar Libet data on the readiness potential, may only show the mind developing alternative possibilities for action just before actually and consciously deciding. The idea that the early RP is already a decision, rather than the forming of an intention, is simply misinterpretation.

The abrupt and rapid decisions to flex a finger measured by Libet bear little resemblance to the kinds of two-stage deliberate decisions for which we can first freely generate alternative possibilities for action, then evaluate which is the best of these possibilities in the light of our reasons, motives, values, and desires - first "free," then "will."

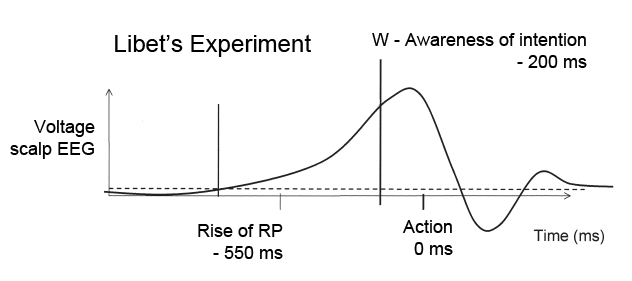
We can correlate the beginnings of the readiness potential (350ms before Libet's conscious will time "W" appears) with the early stage of the two-stage model, when alternative possibilities are being generated, in part at random. The early stage may be delegated to the subconscious, which is capable of considering multiple alternatives (William James' "blooming, buzzing confusion") that would congest the low-data-rate single stream of consciousness.

• Consciousness and the Universe: Quantum Physics, Evolution, Brain & Mind, with Henry Stapp, Roger Penrose

• Toward a Science of Consciousness: The First Tucson Discussions and Debates (Complex Adaptive Systems)

• How quantum brain biology can rescue conscious free will

• The “conscious pilot”—dendritic synchrony moves through the brain to mediate consciousness

• Consciousness in the Universe: Neuroscience, Quantum Space-Time Geometry and Orch OR

• Cytoskeletal Signaling: Is Memory Encoded in Microtubule Lattices by CaMKII Phosphorylation?