|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Grete Hermann John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington James D. Watson John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
John Stachel
John Stachel is Professor Emeritus of Physics and Director of the Center for Einstein Studies at Boston University.
He was the founding editor of the Collected Papers of Albert Einstein, essential documents for understanding the early years of quantum theory, when Einstein invented most of the critical concepts.
His familiarity with Einstein's writings has led him to see how many historians of science have not understood Einstein's contributions to quantum mechanics. And his readings have also led to some provocative interpretations of quantum mechanics.
Bohr and the Photon
In his 1986 article, "Einstein and the Quantum," Stachel developed a "conjecture" that many of the elements of the 2013 "Bohr Atom," specifically energy levles and quantum jumps, were already present in Einstein's 2006 work on anomalous specific heats.
Just as Einstein's 1905 paper is always cited for its explanation of the "photoelectric effect," while his revolutionary "light quantum hypothesis" was mostly ignored, Martin J. Klein tells us that Einstein's 1906 paper was only using specific heat as an application of a much deeper insight into quantum theory. In his paper, Einstein showed that there are energy levels or "states"in matter between which there are transitions that he called "jumps," with the absorption of a quantum of energy hν.
In his 1986 article, "Einstein and the Quantum: Fifty Years of Struggle," Stachel builds on Klein's insight that the specific heat article includes jumps between energy states .He shows that Einstein was interested in spectral lines as early as a 1905 note to Conrad Habicht .
“there is not always a fully developed subject for my musings. At least none that appeals. There would of course be the subject of the spectral lines; but I believe that a simple connection of these phenomena with others already studied does not exist at all, so that the subject for the moment seems to promise very little.”Stachel cites a letter to Philip Lenard a few months later indicating he was following Lenard's studies of atomic spectra. The experiments known to me do not exclude that possibility that the emission or absorption of each individual spectral line is connected with a definite state of the emitting or absorbing center (atom), which [state] is characteristic for it [i.e., the emission or absorption]. ... According to the indicated conception the absorption of a series by a (cold) vapor should be interpreted thus, that the absorption of light of the line ν1 makes the absorbing center in question receptive for light of the line ν2, etc. Then an absorption of ν2 by the vapor would only be possible with simultaneous absorption of ν1.Stachel then interprets Einstein's "musings." This was written after the 1905 paper in which Einstein had proposed that emission and absorption of light of frequency ν be conceived as taking place in quanta of energy hν (actually, Einstein at that time did not use Planck’s h, but the equivalent R/Nβ). Perhaps it is not too far fetched to speculate, based on this letter, that around the end of 1905 Einstein had the idea of discrete energy states (levels, we would say today) of the atom in which it did not radiate. If we multiply ν1 and ν2 by h, we might try to interpret Einstein’s remarks in the letter according to Figure 1 below. 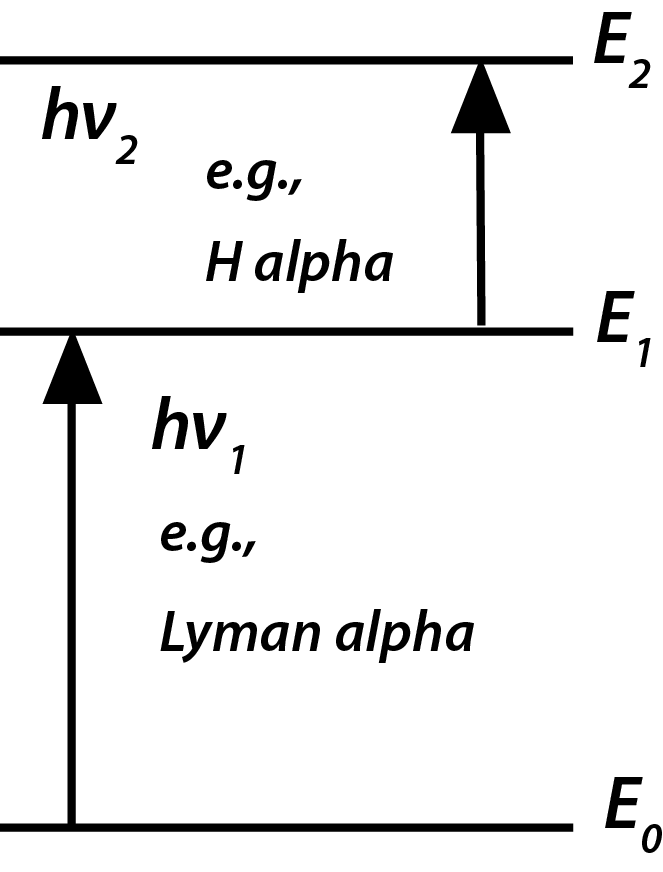 Stachel says that he is not claiming that Einstein anticipated the 1913 Bohr model of the atom, but we have added labels for the Lyman alpha and Balmer alpha lines in the hydrogen atom to Stachel's figure to stress how exact the analogy is to the Bohr atom.
What Einstein is saying is that it is impossible for hydrogen to absorb Hα, the first line in the Balmer series, unless it has first absorbed Lα, the first line in the Lyman series of transitions from the ground state to an excited state.
Stachel says that he is not claiming that Einstein anticipated the 1913 Bohr model of the atom, but we have added labels for the Lyman alpha and Balmer alpha lines in the hydrogen atom to Stachel's figure to stress how exact the analogy is to the Bohr atom.
What Einstein is saying is that it is impossible for hydrogen to absorb Hα, the first line in the Balmer series, unless it has first absorbed Lα, the first line in the Lyman series of transitions from the ground state to an excited state.
The Other Einstein
In his provocative 1993 article, "The Other Einstein: Einstein Contra Field Theory," Stachel cites a number of quotes from Einstein over the years to the effect that the field theory he hoped for might simply be impossible. A field theory implies a continuum with an infinite number of elements. By comparison, Einstein suggested quantum mechanics may be described by an "algebraic theory" with a finite number of discrete elements, that is, the quantum particles themselves such as electrons.
Information philosophy identifies the space-time continuum as an abstract mathematical construct, as immaterial information with which we describe the motions and interactions of discrete, discontinuous, and concrete material particles. The continuum is what Einstein called a "free creation of the human mind." It is an idea.
It is an idea with causal powers. The continuous fields of gravitation (Newton or Einstein) and electromagnetism (Maxwell) tell us the behavior of a test particle at a geometric point, should a particle be there. The quantum wave function is a field that describes the probability of finding a particle at a given point in the continuum. All these continuous fields are determined for all space and time by the distribution of particulate matter in space, the so-called boundary conditions and initial conditions.
Just as general relativity can be seen as curving space, so quantum theory can be seen to add a property to space that "influences" the discrete particles. In Richard Feynman's path-integral formulation of quantum mechanics, the principle of least action explores all space to establish quantum probabilities. Stachel explored this in his 1997 article on Feynman Paths.
There need not be material particles at a point in the ideal space-time continuum in order for us to know the influence on a particle, should there be one present.
Stachel shows that Einstein always considered the possibility that space and time are merely human inventions. As a young man, he very likely read David Hume as saying
"The capacity of the mind is not infinite; consequently no idea of extension or duration consists of an infinite number of parts or inferior ideas, but of a finite number, and these simple and indivisible: ‘Tis therefore possible for space and time to exist conformable to this idea: And if it be possible, ‘tis certain they actually are conformable to it; since their infinite divisibility is utterly impossible and contradictory."Around the time he read Bernhard Riemann to complete his theory of general relativity, Einstein probably noticed that Riemann distinguished between a continuous or discrete manifold. The question of the validity of the postulates of geometry in the indefinitely small is involved in the question concerning the ultimate basis of relations of size in space. In connection with this question, ... the above remark is applicable, namely that while in a discrete manifold the principle of metric relations is implicit in the notion of manifold, it must come from somewhere else in the case of a continuous manifold. Either then the actual things forming the groundwork of space must constitute a discrete manifold, or else the basis of metrical relations must be sought for outside that actuality, in colligating forces that operate upon it. [cf. Source Book in Mathematics, Smith [1929] 1959, 424-25]Noting Einstein's frequent use of Richard Dedekind's phrase "free creations of the human mind" (freie Schöpfungen des menschlichen Geistes), Stachel is sure that Einstein read Dedekind's 1901 argument that all the axioms of Euclid's geometry can be proven with no reference to a continuum between geometric points. If anyone should say that we cannot conceive of space as anything else than continuous, I should venture to doubt it and to call attention to the fact that a far advanced, refined scientific training is demanded in order to perceive clearly the essence of continuity and to comprehend that besides rational quantitative relations, also irrational, and besides algebraic, also transcendental quantitative relations are conceivable. [cf. Dedekind, "The Nature and Meaning of Numbers," in Essays on the Theory of Numbers, 1901, Dover (1963), p.38]Einstein was assuredly familiar with Leopold Kronecker's famous quote "The dear God has made the whole numbers, all the rest is man's work." (Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk). Einstein always had a healthy skepticism about his work on field theory. Stachel points to Einstein's 1923 article “Does Field Theory Offer Possibilities for the Solution of the Quantum Problem?,” in which Einstein points out that the great successes of quantum theory over the last quarter of a century should not be allowed to conceal the lack of any logical foundation for the theory. He quotes Einstein... The essential element of the previous theoretical development, which is characterized by the headings mechanics, Maxwell-Lorentz electrodynamics, theory of relativity, lies in the circumstance that they work with differential equations that uniquely determine events [das Geschehen] in a four-dimensional spatio-temporal continuum if they are known for a spatial cross-section...In view of the existing difficulties, one has despaired of the possibility of describing the actual processes by means of differential equations.The linear Schrödinger differential equation for waves cannot give us the details of individual particles, only the statistics of ensembles of particles . Stachel provides several powerful statements from 1935 to Einstein's posthumous writings pointing toward discrete "algebraic" theories of particles replacing continuum field theories. In any case one does not have the right today to maintain that the foundation must consist in a field theory in the sense of Maxwell. The other possibility, however, leads in my opinion to a renunciation of the time-space continuum and to a purely algebraic physics. Logically this is quite possible (the system is described by a number of integers; “time” is only a possible viewpoint [Gesichtspunkt], from which the other “observables” can be considered—an observable logically coordinated to all the others. Such a theory doesn’t have to be based upon the probability concept. For the present, however, instinct rebels against such a theory (Einstein to Paul Langevin, 3 October 1935, as translated in Stachel 1986, 379-80). It has been suggested that, in view of the molecular structure of all events in the small, the introduction of a space-time continuum may be considered as contrary to nature. Perhaps the success of Heisenberg’s method points to a purely algebraical method of description of nature, to the elimination of continuous functions from physics. Then, however, we must also give up, on principle, the utilization of the space-time continuum. It is not inconceivable that human ingenuity will some day find methods that will make it possible to proceed along this path. Meanwhile, however, this project resembles the attempt to breathe in an airless space (“Physics and Reality,” [1936], cited from Einstein Ideas and Opinions 1954, 319, translation modified). In present-day physics there is manifested a kind of battle between the particle-concept and the field-concept for leadership, which will probably not be decided for a long time. It is even doubtful if one of the two rivals finally will be able to maintain itself as a fundamental concept (Einstein to Herbert Kondo, 11 August 1952, as translated in Stachel 1986, 380). I consider it entirely possible that physics cannot be based upon the field concept, that is on continuous structures. Then nothing will remain of my whole castle in the air including the theory of gravitation, but also nothing of the rest of contemporary physics (Einstein to Besso, 10 August 1954, as translated in ibid., 380). An algebraic theory of physics is affected with just the inverted advantages and weaknesses, aside from the fact that no one has been able to propose a possible logical schema for such a theory. It would be especially difficult to derive something like a spatio-temporal quasi-order from such a schema. I cannot imagine how the axiomatic framework of such a physics would appear, and I don’t like it when one talks about it in dark apostrophes [Anredungen], But I hold it entirely possible that the development will lead there; for it seems that the state of any finite spatially limited system may be fully characterized by a finite number of numbers. This speaks against the continuum with its infinitely many degrees of freedom. The objection is not decisive only because one doesn’t know, in the contemporary state of mathematics, in what way the demand for freedom from singularity (in the continuum theory) limits the manifold of solutions (Einstein to H. S. Joachim, 24 August 1954, as translated in ibid., 581).Stachel wrote "To the end of his life, Einstein was still on the lookout for new mathematical tools that might help turn such speculations, which he thought it best to keep private, into the basis of a real theory. The noted mathematician Abraham Fraenkel reports a conversation that he had with Einstein in 1951. You will see at once why Einstein responded with such interest to what Fraenkel told him:" In December 1951 I had the privilege of talking to Professor Einstein and describing the recent controversies between the (neo-) intuitionists and their “formalistic” and “logistic” antagonists; I pointed out that the first attitude would mean a kind of atomistic theory of functions, comparable to the atomistic structure of matter and energy. Einstein showed a lively interest in the subject and pointed out that to the physicist such a theory would seem by far preferable to the classical theory of continuity. I objected by stressing the main difficulty, namely, the fact that the procedures of mathematical analysis, e.g., of differential equations, are based on the assumption of mathematical continuity, while a modification sufficient to cover an intuitionistic- discrete medium cannot easily be imagined. Einstein did not share this pessimism and urged mathematicians to try to develop suitable new methods not based on continuity (Fraenkel 1954).And Stachel concluded his provocative essay on the "Other Einstein" with these worlds... "It is now time to bring my story to a close. Perhaps I may best do so by reminding the reader of Einstein’s last published words—the final words of the posthumously published “Appendix Two” to the fifth edition of The Meaning of Relativity:" One can give good reasons why reality cannot at all be represented by a continuous field. From the quantum phenomena it appears to follow with certainty that a finite system of finite energy can be completely described by a finite set of numbers (quantum numbers). This does not seem to be in accordance with a continuum theory, and must lead to an attempt to find a purely algebraic theory for the description of reality. But nobody knows how to obtain the basis of such a theory. (Einstein 1955, 166).Stachel concludes, "Einstein had decided to voice his skepticism about the continuum at the very moment when he was presenting the last version of his final unified field theory. The Other Einstein had the last word."
Misattributions of Einstein's Work
In a talk given March 11,1986 at “A Centenary Symposium: In Memory of Niels Bohr" of the Boston Colloquium for the Philosophy of Science, Stachel reported that modern textbooks frequently refer to the Bohr atom as emitting and absorbing photons. While this is intuitively understandable for the modern physicist who knows all about atoms and photons, Stachel found a prominent physicist who claimed that Bohr himself assumed photons were involved.
I started to survey textbook discussions of the Bohr atom, to see how they present the relation between Bohr’s work on the hydrogen atom"and Einstein’s light quantum hypothesis. The first book at which I looked is so perfect an example of what I expected to find that I stopped my search—lest further research invalidate my belief that the presentation in one of the best texts available, Arnold B. Arons’ Development of the Concepts of Physics is typical of many others. After quoting from the opening of Bohr’s classic 1913 paper, Arons continues:We can extend Stachel's survey with the following quotations from texts since the early 1930's to current editions of the most popular college textbooks:With this background of motivation, Bohr suggested a direct application of Einstein’s photon hypothesis in the following manner: (1) Abandon classical electrodynamics to the extent of assuming that at radii of atomic dimensions ... electrons can revolve in stable orbits without continuously radiating energy in the form of electromagnetic waves .... (2) Invoking Einstein’s heuristic model, assume that electromagnetic radiation is absorbed or emitted in transfer of electrons from one orbit to another and that such absorption and emission of energy by individual electrons is associated with absorption or emission of individual photons or radiation quanta of energy hv - as suggested by Einstein’s heuristic explanation of the photoelectric effect [3, p. 856],The actual story is quite different, of course. It would be more correct to say (but still not really accurate) that Bohr was an inveterate opponent of the photon concept until 1925, when the results of Bothe-Geiger and Compton-Simon experiments forced him to incorporate the photon concept into his thinking. My purpose here is to document in some detail the story of Bohr and the photon, providing the nuances that are missing from straw-man story I have just told. I think the full story is worth telling, because it provides much of the raw material for a better understanding of how Bohr developed his views on correspondence and complementarity; and, although I shall not elaborate much on this theme, how he later understood and applied them. Einstein’s hypothesis found many supports. One of these comes from the structure of atoms. Atoms emit monochromatic spectrum lines, falling often into regular series. Bohr was able to explain this, at least in hydrogen, the simplest atom, by assuming that the atom was capable of existing only in certain definite stationary states, each of a definite energy. He supposed that radiation was not emitted continuously, as the electromagnetic field from a rotating or vibrating particle would be, but that the atom stayed in one energy level until it suddenly made a jump to a second, lower, level, with emission of a photon. If the higher energy is E2, the lower E1, the energy of the photon would be E2 — E1, so that its frequency would be E2/h — E1/h. This formula has proved to be justified by great amounts of experimental material. First, it states that the frequencies emitted by atoms should be the differences of “terms” E/h, each referring to an energy level of the atom. In trying to explain this unique character of light emitted by free atoms Bohr found that it was completely impossible if he assumed that the electrons circulate around the nucleus according to Newton’s laws of motion in the same way that the planets revolve around the sun. He was thus led to setting up a separate hypothesis, with which he modified Newton’s laws in much the same way that Planck had done in explaining properties of heat radiation. Bohr assumed that only certain discrete sets of circular orbits (preferred orbits) were allowed for the electrons moving around the nucleus. Electrons in different orbits had different energies, and when an electron jumped from one of higher to one of lower energy, the difference in energy was emitted in the form of a light quantum (photon). This concept of emission of photons may be considered as a sort of inversion of Einstein’s photoelectric law, in which a photon is absorbed and an electron liberated. Bohr’s reasoning went like this. The emission line spectrum of an element tells us that atoms of that element emit photons with only certain specific frequencies and hence certain specific energies E = hf. During the emission of a photon, the internal energy of the atom changes by an amount equal to the energy of the photon. Therefore, said Bohr, each atom must be able to exist with only certain specific values of internal energy. Each atom has a set of possible energy' levels. An atom can have an amount of internal energy equal to any one of these levels, but it cannot have an energy intermediate between two levels. All isolated atoms of a given element have the same set of energy levels, but atoms of different elements have different sets. Suppose an atom is raised, or excited, to a high energy level. (In a hot gas this happens when fast-moving atoms undergo inelastic collisions with each other or with the walls of the gas container. In an electric discharge tube, such as those used in a neon light fixture, atoms are excited by collisions with fast-moving electrons.) According to Bohr, an excited atom can make a transition from one energy level to a lower level by emitting a photon with energy equal to the energy difference between the initial and final levels.
Historians of Einstein's Physics
Stachel's important predecessors on Einstein's contributions were Martin J. Klein and Abraham Pais. And since Stachel there is the very important work of A. Douglas Stone. We are building a table of comparison positions on seven major contributions by Einstein that are often credited to others. We rate the clarification by each author of Einstein's position, and will quote from each historian on another page.
References
"Einstein and the quantum: fifty years of struggle," in From quarks to quasars: Philosophical problems of modern physics, 349-81. (1986).
"Einstein and Quantum Mechanics," in Conceptual Problems Quantum Gravity, Birkhäuser, (1991)
"The Other Einstein: Einstein contra field theory," in Science in Context, 6(1), 275-290. (1993), in Einstein from "B" to "Z", p.141-154.
"Feynman paths and quantum entanglement: Is there any more to the mystery," in Potentiality, Entanglement and Passion-at-a-Distance (pp. 245-256). Springer Netherlands.(1997).
Einstein from "B" to "Z", Birkhäuser, (2002)
"Bohr and the Photon," in Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle, 69-83. (2009).
Normal | Teacher | Scholar
|