Probability was introduced as an acceptable euphemism for
chance in the eighteenth century, by
Pierre-Simon Laplace, for example, who called his work the "calculus of probabilities."
The root meaning of probability was originally "approbation." Something probable was deserving of belief. This connotation has been lost in modern times as the understanding of mathematical probabilities has become widespread. Although some epistemologists still connect "degrees of belief" with epistemic probabilities.
We can distinguish probability from
statistics by reserving the term probability for the
a priori or epistemic sense of the term.
Probabilities are a priori theories. Statistics are a posteriori experiments.
The
a priori probability of two dice showing two sixes is 1/36.
A priori probability assumes that we have no
information that favors one outcome over the others. This is the
principle of indifference or
principle of insufficient reason. Specifically, it assumes that all outcomes are equally probable. In short, all other things being equal, things are equal.
If we did have information about a difference, we would adjust our probabilities. The increase in our
information or "state of knowledge" is the essential idea in
Bayesian probability.
And how might we come by such additional information? By running experimental trials and gathering data on the frequencies of real outcomes. This is the work of statistics.
In the theory of measurements and measurement errors, we find a dispersion in measurements when we are measuring the same thing over and over. These are measurement errors. It is very important to distinguish measurement errors from real variations in the thing measured. But this is not easy, because errors and the natural distribution in values of a measured property normally follow the same distribution function.
If the values of some property in a population is the consequence of independent random events, for example coin flips that result in heads instead of tails, the distribution can be shown to follow the well-known bell-shaped curve or "normal" distribution.
Pr(x) = (1/√(2π)) e-x2/2
Observational errors themselves are the result of independent random factors, so they follow the same distribution.
This distribution function was discovered in the 1720's by the French mathematician
Abraham de Moivre. It was identified with measurement errors by astronomers measuring star positions in the early nineteenth century, notably by the Belgian astronomer
Adolphe Quételet.
An unfortunate choice of terms led to this being called the "
law of errors." Mathematicians and philosophers both jumped to the erroneous conclusion that if random events followed "laws" that they must in fact be determined by those laws.
De Moivre's work was a famous book called "The Doctrine of Chances." In the 1738 edition he found that in the limit of large numbers of tosses of a coin, the discrete binomial expansion of (
p -
q)
n could be approximated by a continuous mathematical curve (the modern bell curve).
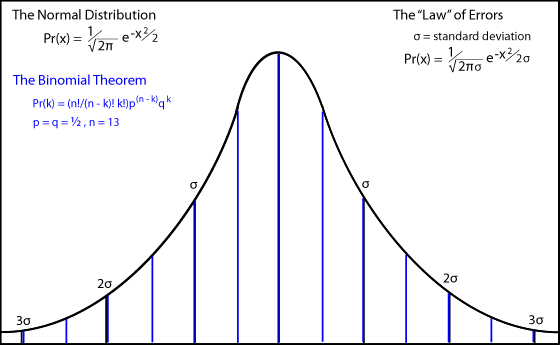
This was an era when mathematical analysis and continuity carried an aura of deterministic causal truth, compared to the chance nature of individual random events.
The curve was first called the "normal distribution" by
Charles Sanders Peirce, who better than any other philosopher articulated the difference between
a priori probabilities and
a posteriori statistics.
For reasons that are philosophically and physically very deep (basically the fundamental discreteness of nature), we find a similar random distribution of many physical, biological, and social characteristics. Note that the distribution of such characteristics is
ontological, not
epistemic. It is not a matter of what humans can know, but how things are in a mind-independent external world..
Social scientists in the early nineteenth century argued that randomness in many populations was governed by this "law."
Adolphe Quetelet was a Belgian astronomer who developed the error distribution as a way to analyze and reduce the data from astronomical observations. He then found the same distribution function in many human statistics, the number of marriages and suicides per year, for example. He found "norms for many human characteristics, such as height, and promoted the concept of the average man (
l'homme moyen) . Quetelet and other social scientists mistakenly concluded that the "lawfulness" of these normal distributions affirmed the fundamental
deterministic nature of the world.
To the modern sensibility, an argument that all events are determined
because their characteristics are random and normally distributed seems illogical and a bit perverse. But such was the philosophical and religious commitment of nineteenth-century scientists to the
many forms of determinism.
If just one single event is determined by chance, then
indeterminism would be true, some philosophers say, which would undermine the very possibility of certain knowledge. Some go to the extreme of saying that chance makes the state of the world totally independent of any earlier states, which is nonsense, but it shows how anxious they are about chance.
In statistical mechanics, the state of least information (equilibrium) can be achieved in many more ways than states with recognizable information. The equilibrium macrostate has the most microstates, each assumed to have equal
a priori probability. If a system begins in an initially ordered state (high information), it tends to evolve toward states of disorder (absence of microscopic information). The increase of entropy (second law of thermodynamics) is then seen to be a decrease of information. The mathematical equations for entropy and information turn out to be identical apart from their sign and arbitrary constants.
Both are proportional to the logarithm of the number W of microstates consistent with the macrostate information.
I ∝ -S ∝ lnW
Both
James Clerk Maxwell and
Ludwig Boltzmann were familiar with the work of
Adolph Quételet and his English colleague
Thomas Buckle. Maxwell, and probably Boltzmann too, used the above law of distribution of random events in the limit of large numbers to help them derive the law for the distribution of molecular velocities in a gas.
For Scholars
To hide this material, click on the Teacher or Normal link.
Aristotle on Probability, Rheetoric, Book II, Chapter 24, section 10, line 1402a2
[9]
ἄλλος παρὰ τὴν ἔλλειψιν τοῦ πότε καὶ πῶς,
οἷον ὅτι δικαίως Ἀλέξανδρος ἔλαβε τὴν Ἑλένην: αἵρεσις γὰρ αὐτῇ ἐδόθη παρὰ τοῦ πατρός. οὐ γὰρ ἀεὶ ἴσως, ἀλλὰ τὸ πρῶτον: καὶ γὰρ ὁ πατὴρ μέχρι τούτου κύριος.
ἢ εἴ τις φαίη τὸ τύπτειν τοὺς ἐλευθέρους ὕβριν εἶναι: οὐ γὰρ πάντως, ἀλλ᾽ ὅταν ἄρχῃ χειρῶν ἀδίκων.
[10]
ἔτι ὥσπερ ἐν τοῖς ἐριστικοῖς παρὰ τὸ ἁπλῶς καὶ μὴ ἁπλῶς, ἀλλὰ τί, γίγνεται φαινόμενος
συλλογισμός, οἷον ἐν μὲν τοῖς διαλεκτικοῖς ὅτι ἔστι τὸ μὴ ὄν [ὄν], ἔστι γὰρ τὸ μὴ ὂν μὴ ὄν, καὶ ὅτι ἐπιστητὸν τὸ ἄγνωστον, ἔστιν γὰρ ἐπιστητὸν τὸ ἄγνωστον ὅτι ἄγνωστον, οὕτως καὶ ἐν τοῖς ῥητορικοῖς ἐστιν φαινόμενον ἐνθύμημα παρὰ τὸ μὴ ἁπλῶς εἰκὸς ἀλλὰ τὶ εἰκός. ἔστιν δὲ τοῦτο οὐ καθόλου, ὥσπερ
καὶ Ἀγάθων λέγει
“τάχ᾽ ἄν τις εἰκὸς αὐτὸ τοῦτ᾽ εἶναι λέγοι,
βροτοῖσι πολλὰ τυγχάνειν οὐκ εἰκότα.
” γίγνεται γὰρ τὸ παρὰ τὸ εἰκός, ὥστε εἰκὸς καὶ τὸ παρὰ τὸ εἰκός, εἰ δὲ τοῦτο, ἔσται τὸ μὴ εἰκὸς εἰκός. ἀλλ᾽ οὐχ ἁπλῶς,
ἀλλ᾽ ὥσπερ καὶ ἐπὶ τῶν ἐριστικῶν τὸ κατὰ τί καὶ πρὸς τί καὶ πῇ οὐ προστιθέμενα ποιεῖ τὴν συκοφαντίαν, καὶ ἐνταῦθα παρὰ τὸ εἰκὸς εἶναι μὴ ἁπλῶς ἀλλὰ τὶ εἰκός.
[11] ἔστι δ᾽ ἐκ τούτου τοῦ τόπου ἡ Κόρακος τέχνη συγκειμένη: “ἄν τε γὰρ μὴ ἔνοχος ᾖ τῇ αἰτίᾳ, οἷον ἀσθενὴς ὢν αἰκίας φεύγει (οὐ γὰρ εἰκός), κἂν ἔνοχος
ᾖ, οἷον ἰσχυρὸς ὤν (οὐ γὰρ εἰκός, ὅτι εἰκὸς ἔμελλε δόξειν)”. ὁμοίως δὲ καὶ ἐπὶ τῶν ἄλλων: ἢ γὰρ ἔνοχον ἀνάγκη ἢ μὴ ἔνοχον εἶναι τῇ αἰτίᾳ: φαίνεται μὲν οὖν ἀμφότερα εἰκότα, ἔστι δὲ τὸ μὲν εἰκός, τὸ δὲ οὐχ ἁπλῶς ἀλλ᾽ ὥσπερ εἴρηται: καὶ τὸ τὸν ἥττω δὲ λόγον κρείττω ποιεῖν τοῦτ᾽ ἔστιν. καὶ
ἐντεῦθεν δικαίως ἐδυσχέραινον οἱ ἄνθρωποι τὸ Πρωταγόρου ἐπάγγελμα: ψεῦδός τε γάρ ἐστιν, καὶ οὐκ ἀληθὲς ἀλλὰ φαινόμενον εἰκός, καὶ ἐν οὐδεμιᾷ τέχνῃ ἀλλ᾽ <ἢ> ἐν ῥητορικῇ καὶ ἐριστικῇ.
[10] Further, as in sophistical disputations, an apparent syllogism arises as the result of considering a thing first absolutely, and then not absolutely, but only in a particular case. For instance, in Dialectic, it is argued that that which is not is, for that which is not is that which is not1; also, that the unknown can be known, for it can be known of the unknown that it is unknown. Similarly, in Rhetoric, an apparent enthymeme may arise from that which is not absolutely probable but only in particular cases. But this is not to be understood absolutely, as Agathon says:
“ One might perhaps say that this very thing is probable,
that many things happen to men that are not probable;
” for that which is contrary to probability nevertheless does happen, so that that which is contrary to probability is probable. If this is so, that which is improbable will be probable. But not absolutely; but as, in the case of sophistical disputations, the argument becomes fallacious when the circumstances, reference, and manner are not added, so here it will become so owing to the probability being not probable absolutely but only in particular cases.
1 The first “is” means “has a real, absolute existence”; the second “is” merely expresses the identity of the terms of the proposition, and is particular; but the sophistical reasoner takes it in the same sense as the first. The same applies to the argument about the unknown.
 This was an era when mathematical analysis and continuity carried an aura of deterministic causal truth, compared to the chance nature of individual random events.
The curve was first called the "normal distribution" by Charles Sanders Peirce, who better than any other philosopher articulated the difference between a priori probabilities and a posteriori statistics.
For reasons that are philosophically and physically very deep (basically the fundamental discreteness of nature), we find a similar random distribution of many physical, biological, and social characteristics. Note that the distribution of such characteristics is ontological, not epistemic. It is not a matter of what humans can know, but how things are in a mind-independent external world..
Social scientists in the early nineteenth century argued that randomness in many populations was governed by this "law." Adolphe Quetelet was a Belgian astronomer who developed the error distribution as a way to analyze and reduce the data from astronomical observations. He then found the same distribution function in many human statistics, the number of marriages and suicides per year, for example. He found "norms for many human characteristics, such as height, and promoted the concept of the average man (l'homme moyen) . Quetelet and other social scientists mistakenly concluded that the "lawfulness" of these normal distributions affirmed the fundamental deterministic nature of the world.
To the modern sensibility, an argument that all events are determined because their characteristics are random and normally distributed seems illogical and a bit perverse. But such was the philosophical and religious commitment of nineteenth-century scientists to the many forms of determinism.
If just one single event is determined by chance, then indeterminism would be true, some philosophers say, which would undermine the very possibility of certain knowledge. Some go to the extreme of saying that chance makes the state of the world totally independent of any earlier states, which is nonsense, but it shows how anxious they are about chance.
In statistical mechanics, the state of least information (equilibrium) can be achieved in many more ways than states with recognizable information. The equilibrium macrostate has the most microstates, each assumed to have equal a priori probability. If a system begins in an initially ordered state (high information), it tends to evolve toward states of disorder (absence of microscopic information). The increase of entropy (second law of thermodynamics) is then seen to be a decrease of information. The mathematical equations for entropy and information turn out to be identical apart from their sign and arbitrary constants.
Both are proportional to the logarithm of the number W of microstates consistent with the macrostate information.
This was an era when mathematical analysis and continuity carried an aura of deterministic causal truth, compared to the chance nature of individual random events.
The curve was first called the "normal distribution" by Charles Sanders Peirce, who better than any other philosopher articulated the difference between a priori probabilities and a posteriori statistics.
For reasons that are philosophically and physically very deep (basically the fundamental discreteness of nature), we find a similar random distribution of many physical, biological, and social characteristics. Note that the distribution of such characteristics is ontological, not epistemic. It is not a matter of what humans can know, but how things are in a mind-independent external world..
Social scientists in the early nineteenth century argued that randomness in many populations was governed by this "law." Adolphe Quetelet was a Belgian astronomer who developed the error distribution as a way to analyze and reduce the data from astronomical observations. He then found the same distribution function in many human statistics, the number of marriages and suicides per year, for example. He found "norms for many human characteristics, such as height, and promoted the concept of the average man (l'homme moyen) . Quetelet and other social scientists mistakenly concluded that the "lawfulness" of these normal distributions affirmed the fundamental deterministic nature of the world.
To the modern sensibility, an argument that all events are determined because their characteristics are random and normally distributed seems illogical and a bit perverse. But such was the philosophical and religious commitment of nineteenth-century scientists to the many forms of determinism.
If just one single event is determined by chance, then indeterminism would be true, some philosophers say, which would undermine the very possibility of certain knowledge. Some go to the extreme of saying that chance makes the state of the world totally independent of any earlier states, which is nonsense, but it shows how anxious they are about chance.
In statistical mechanics, the state of least information (equilibrium) can be achieved in many more ways than states with recognizable information. The equilibrium macrostate has the most microstates, each assumed to have equal a priori probability. If a system begins in an initially ordered state (high information), it tends to evolve toward states of disorder (absence of microscopic information). The increase of entropy (second law of thermodynamics) is then seen to be a decrease of information. The mathematical equations for entropy and information turn out to be identical apart from their sign and arbitrary constants.
Both are proportional to the logarithm of the number W of microstates consistent with the macrostate information.

